减色混合是通过颜料选择性吸收光波产生色彩的物理过程，其数学模型为印刷、涂料和纺织等行业提供了精确的色彩控制基础。本文简单总结了减色混合理论与公式体系。

理论框架与光学基础

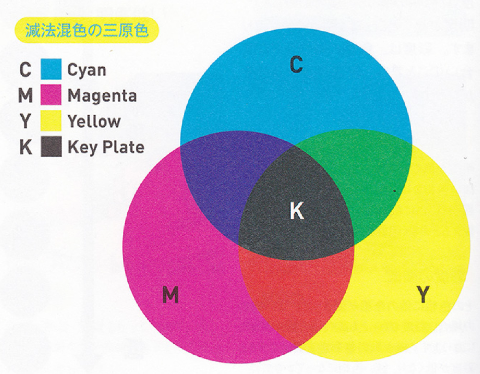
光吸收与散射模型

Kubelka-Munk理论是减色混合的基石，描述颜料层的光学行为。对于单一颜料，反射率R与吸收系数K、散射系数S的关系为：

K/S = (1-R∞)²/2R∞

其中R∞为无限厚度的反射率。对于多颜料混合，总吸收系数和散射系数为各颜料加权和：

Kmix = ΣciKi

Smix = ΣciSi

ci为各颜料浓度。该模型准确预测颜料混合后的颜色，广泛应用于涂料、塑料等行业配色。

比尔-朗伯定律解释透明层的色彩变化。光强衰减公式为 I = I₀e^(-μx)，其中μ为线性吸收系数，x为厚度。对于染料溶液，浓度c与吸光度A的关系为 A = εcl，ε为摩尔吸光系数，l为光程。这为透明介质配色提供理论依据。

颜色预测与配方计算

基于K-M理论的颜色预测流程包括：测量基础颜料的光学常数（K、S）→计算目标颜色的K/S值→解方程组求各颜料浓度。现代配色软件采用矩阵运算：

[K/S]target = C·[K/S]sample

其中C为浓度矩阵。迭代优化算法（如最小二乘法）求解最优配方，满足成本、性能等多目标约束。

对于不透明材料，遮盖力与对比率相关。对比率公式为 CR = Rg/Rw，其中Rg为黑色背景反射率，Rw为白色背景反射率。CR≥0.98时认为完全遮盖，颜料用量与遮盖面积成反比。

减色混合公式体系与应用参数

实际应用与计算实例

印刷行业的网点混合

印刷采用网点面积率混合模型。根据纽介堡方程，混合色三刺激值为：

X = ΣaiXi

Y = ΣaiYi

Z = ΣaiZi

其中ai为第i种油墨网点面积率，Xi、Yi、Zi为该油墨的三刺激值。对于四色印刷，需解16个方程组成的方程组，现代软件采用查找表法加速计算。

网点扩大补偿是关键技术。根据ISO 12647-2标准，50%网点的扩大值控制在8%-12%。补偿曲线公式为 ac = f(ad)，其中ad为设计网点面积率，ac为校正后输出值。柔性版印刷补偿量可达15%-20%，胶印为3%-8%。

涂料配方的光学计算

涂料配色采用双常数库贝尔卡-芒克理论。先测量钛白粉和各色浆的K、S值，建立光学常数数据库。目标颜色的K/S值计算为：

(K/S)target = (1-Rtarget)²/2Rtarget

然后求解线性方程组：

Kmix = cwKw + ΣciKi

Smix = cwSw + ΣciSi

其中cw为白色颜料浓度，ci为色浆浓度。计算机迭代计算满足ΔE*ab≤1.0的最优配方，同时考虑成本最低化。

颜料着色力按ISO 787-24标准测试。着色强度公式为 IS = (K/S)sample/(K/S)standard，标准样品为1.0。高着色力颜料可达1.5-2.0，减少用量降低成本。

特殊混合现象与边界条件

颜料相互作用

颜料混合存在非线性效应。当颜料折射率不匹配时，会发生散射损失，实际反射率低于理论值。补偿公式为：

Ractual = Rtheory - ΔRinteraction

相互作用系数ΔR通过实验测定，通常为0.02-0.05。

荧光颜料混合需特殊处理。斯托克斯位移导致吸收和发射光谱重叠，配色公式修正为：

Rfluorescent = Rabsorption + Remission

需用蒙特卡洛方法模拟光子传输路径，计算复杂但精度更高。

介质影响与表面效应

连接料折射率影响颜色强度。根据菲涅耳公式，反射损失与折射率差相关：

F = (n1-n2)²/(n1+n2)²

高折射率树脂（n=1.6-1.7）比低折射率（n=1.4-1.5）提供更高色彩饱和度。

表面粗糙度导致光散射。根据朗伯余弦定律，粗糙表面反射更分散，明度降低。光泽度与粗糙度的关系为：

G = Gmax·exp(-σ²/λ²)

其中σ为表面粗糙度均方根，λ为光波长。哑光处理需控制σ在0.5-1.0μm。